==作者:cybsky==
[toc]
说明
Redis中没有对跳表完全理解,特此补充一篇文章记录对跳表的学习.
有序单链表
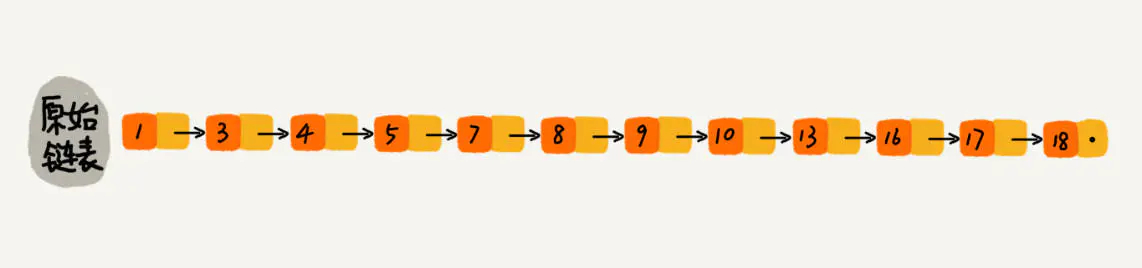
下图是一个简单的有序单链表,单链表的特性就是每个元素存放下一个元素的引用。即:通过第一个元素可以找到第二个元素,通过第二个元素可以找到第三个元素,依次类推,直到找到最后一个元素。想快速找到下图链表中的 10 这个元素,只能从头开始遍历链表,直到找到我们需要找的元素。查找路径:1、3、4、5、7、8、9、10。这样的查找效率很低,平均时间复杂度很高O(n)。
跳表
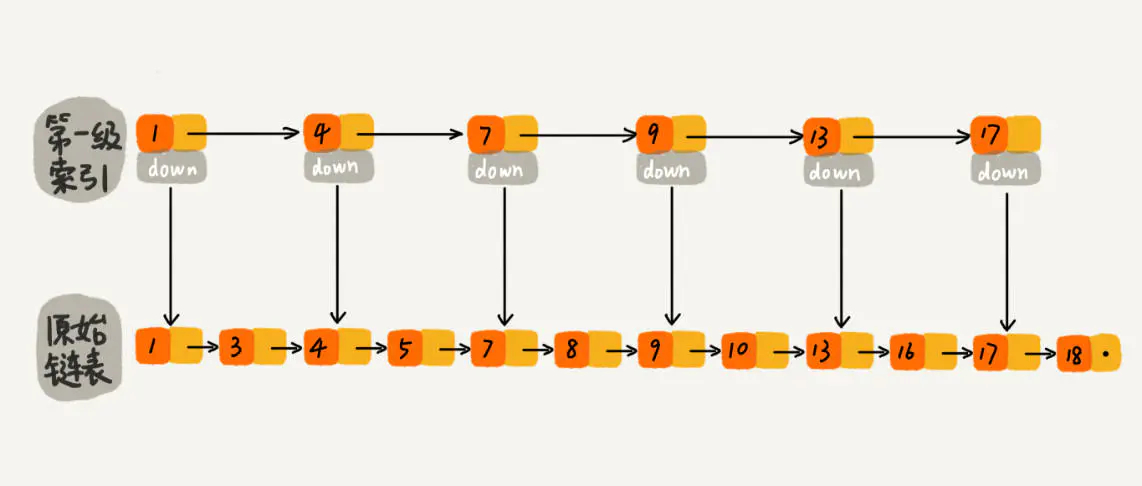
我们从链表中每两个元素抽出来,加一级索引,一级索引指向了原始链表。查找时先在索引找 1、4、7、9,遍历到一级索引的 9 时,发现 9 的后继节点是 13,比 10 大,于是不往后找了,而是通过 9 找到原始链表的 9,然后再往后遍历找到了我们要找的 10,遍历结束。加了一级索引后,查找路径:1、4、7、9、10,查找节点需要遍历的元素相对少了,我们不需要对 10 之前的所有数据都遍历,查找的效率提升了。
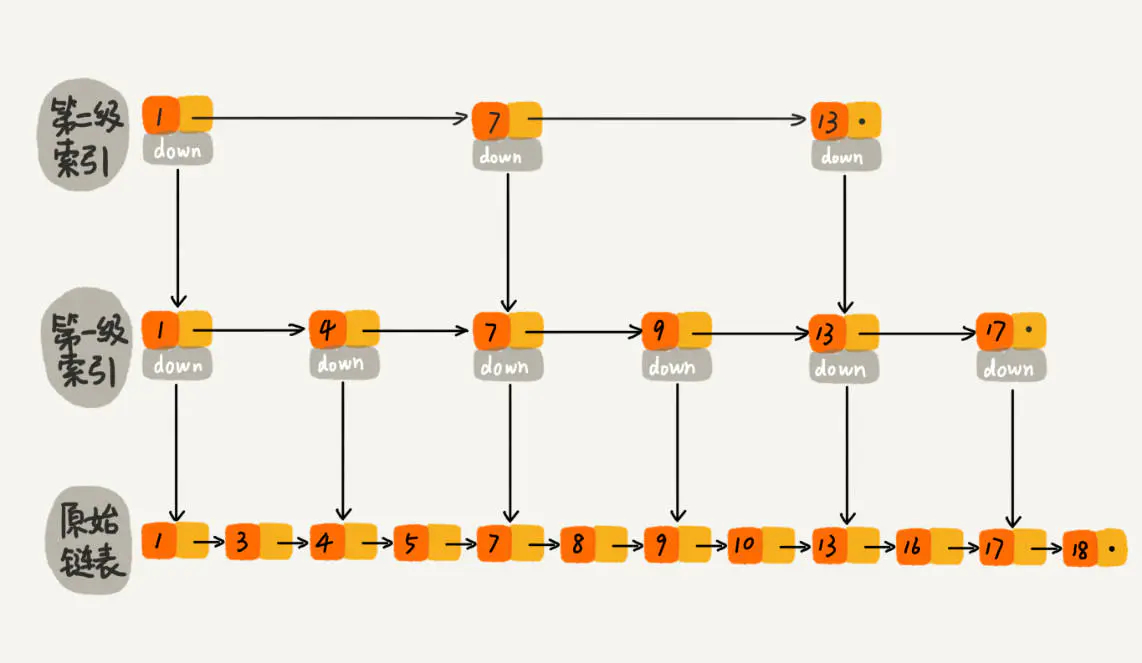
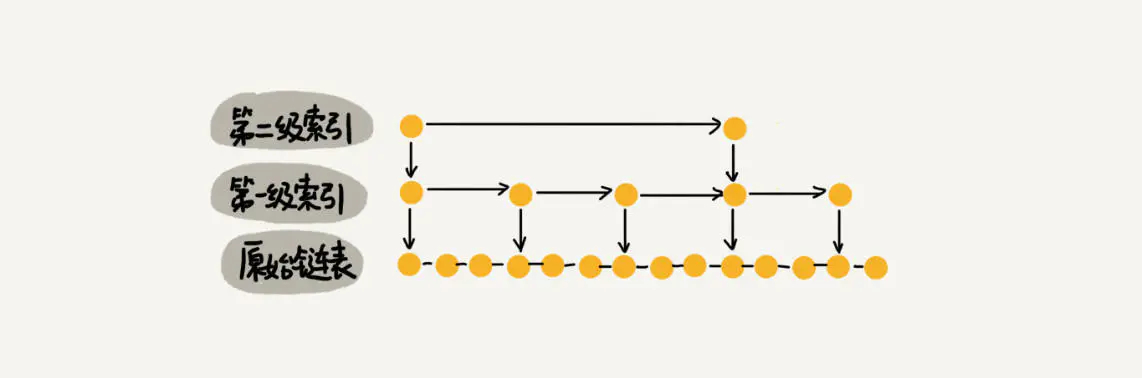
那如果加二级索引呢?如下图所示,查找路径:1、7、9、10。是不是找 10 的效率更高了?这就是跳表的思想,用“空间换时间”,通过给链表建立索引,提高了查找的效率。
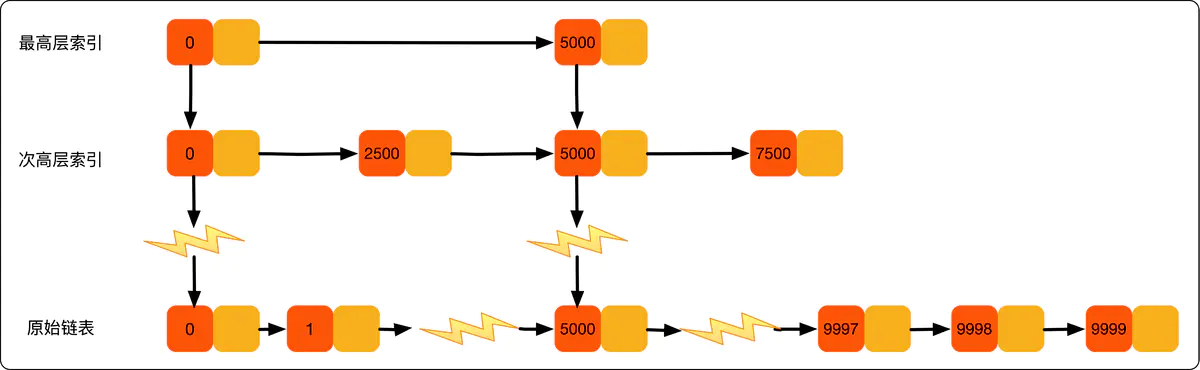
当元素数量较多时,索引提高的效率比较大,近似于二分查找。
到这里大家应该已经明白了什么是跳表。跳表是可以实现二分查找的有序链表。
跳表的查找时间复杂度
先来求跳表的索引高度。如下图所示,假设每两个结点会抽出一个结点作为上一级索引的结点,原始的链表有n个元素,则一级索引有n/2 个元素、二级索引有 n/4 个元素、k级索引就有 n/2k个元素。最高级索引一般有2个元素,即:最高级索引 h 满足 2 = n/2h,即 h = log2n - 1,最高级索引 h 为索引层的高度加上原始数据一层,跳表的总高度 h = log2n。
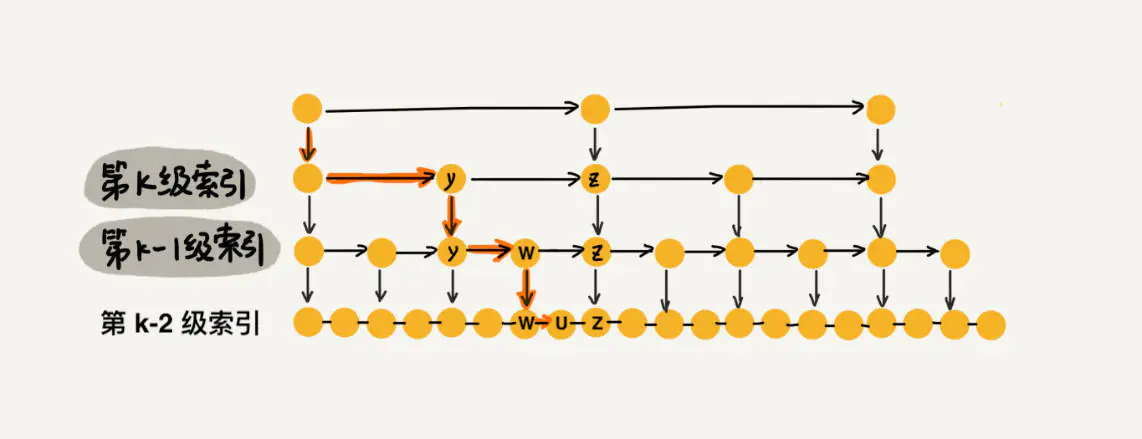
每级索引中都是两个结点抽出一个结点作为上一级索引的结点,每一层最多遍历3个结点。跳表的索引高度 h = log2n,且每层索引最多遍历 3 个元素。所以跳表中查找一个元素的时间复杂度为 O(3*logn),省略常数即:O(logn)。
跳表的空间复杂度
假如原始链表包含 n 个元素,则一级索引元素个数为 n/2、二级索引元素个数为 n/4、三级索引元素个数为 n/8 以此类推。所以,索引节点的总和是:n/2 + n/4 + n/8 + … + 8 + 4 + 2 = n-2,**空间复杂度是 O(n)**。
如下图所示:如果每三个结点抽一个结点做为索引,索引总和数就是 n/3 + n/9 + n/27 + … + 9 + 3 + 1= n/2,减少了一半。所以我们可以通过较少索引数来减少空间复杂度,但是相应的肯定会造成查找效率有一定下降,我们可以根据我们的应用场景来控制这个阈值,看我们更注重时间还是空间。
But,索引结点往往只需要存储 key 和几个指针,并不需要存储完整的对象,所以当对象比索引结点大很多时,索引占用的额外空间就可以忽略了。举个例子:我们现在需要用跳表来给所有学生建索引,学生有很多属性:学号、姓名、性别、身份证号、年龄、家庭住址、身高、体重等。学生的各种属性只需要在原始链表中存储一份即可,我们只需要用学生的学号(int 类型的数据)建立索引,所以索引相对原始数据而言,占用的空间可以忽略。
插入数据
插入数据看起来也很简单,跳表的原始链表需要保持有序,所以我们会向查找元素一样,找到元素应该插入的位置。如下图所示,要插入数据6,整个过程类似于查找6,整个的查找路径为 1、1、1、4、4、5。查找到第底层原始链表的元素 5 时,发现 5 小于 6 但是后继节点 7 大于 6,所以应该把 6 插入到 5 之后 7 之前。整个时间复杂度为查找元素的时间复杂度 O(logn)。
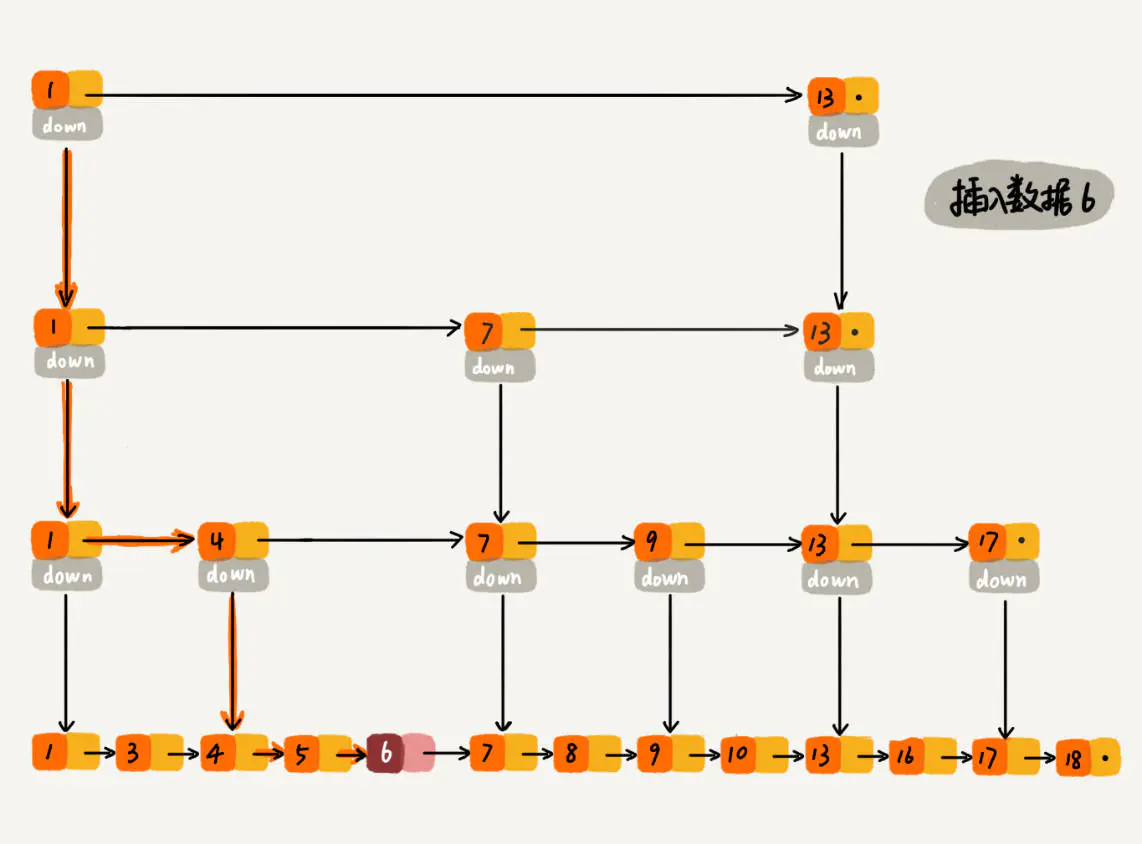
如下图所示,假如一直往原始列表中添加数据,但是不更新索引,就可能出现两个索引节点之间数据非常多的情况,极端情况,跳表退化为单链表,从而使得查找效率从 O(logn) 退化为 O(n)。
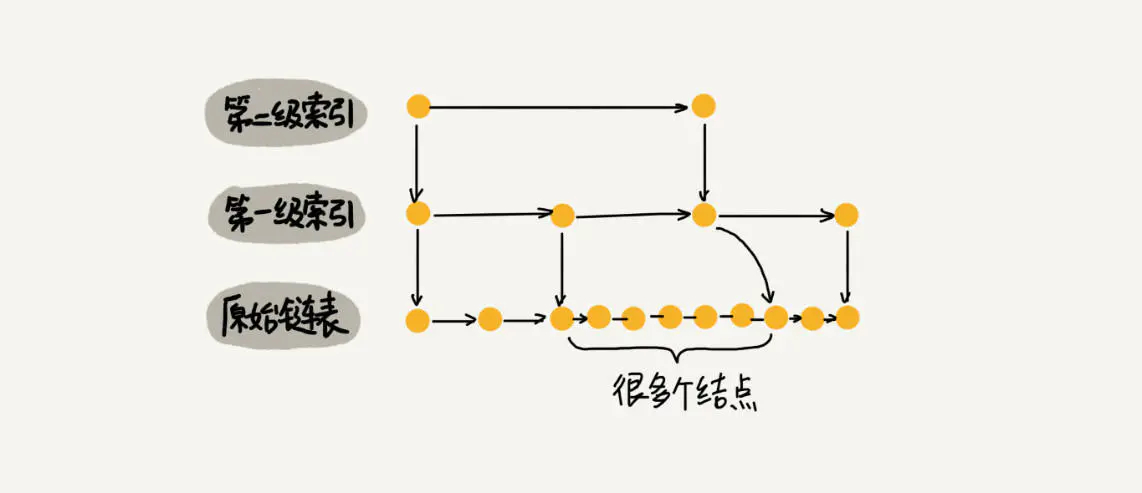
我们该如何去维护这个索引呢?比较容易理解的做法就是完全重建索引,我们每次插入数据后,都把这个跳表的索引删掉全部重建,重建索引的时间复杂度是多少呢?因为索引的空间复杂度是 O(n),即:索引节点的个数是 O(n) 级别,每次完全重新建一个 O(n) 级别的索引,时间复杂度也是 O(n) 。造成的后果是:为了维护索引,导致每次插入数据的时间复杂度变成了 O(n)。
一个比较好的方法是使用随机函数:当我们往跳表中插入数据的时候,我们可以选择同时将这个数据插入到部分索引层中。如何选择加入哪些索引层呢?我们通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值 K,那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。
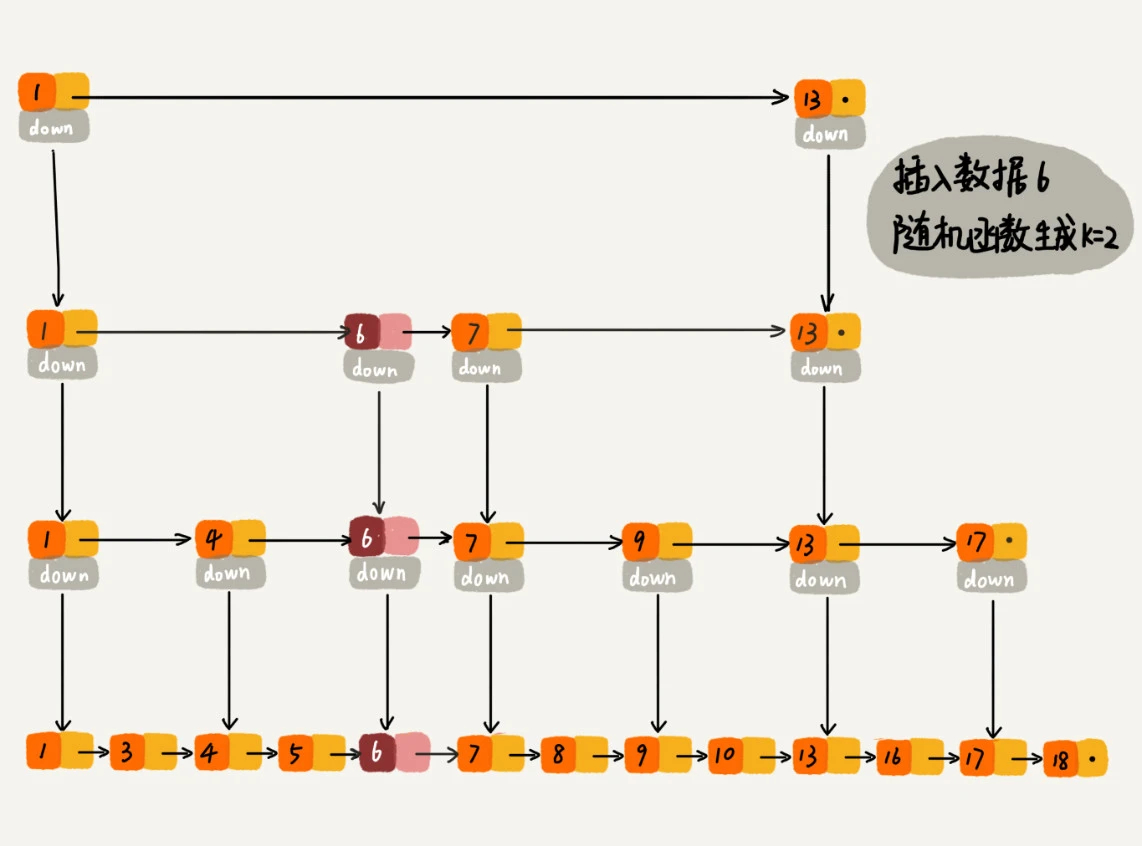
随机函数的选择很有讲究,从概率上来讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能过度退化。
